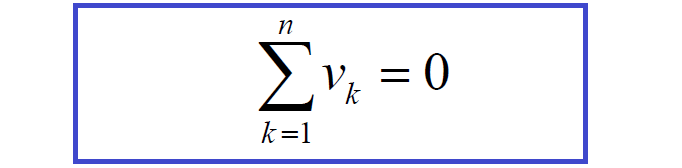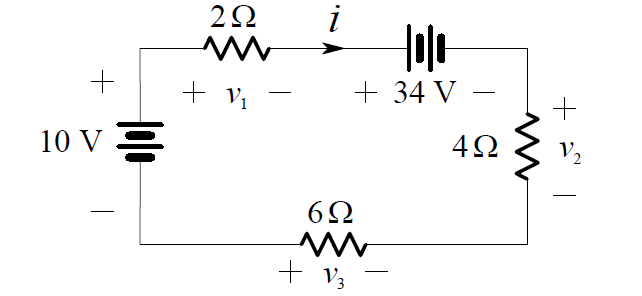Starting at any node in a circuit, we form a loop by traversing through elements (open-circuits included!) and returning to the starting node, never encountering any other node more than once.
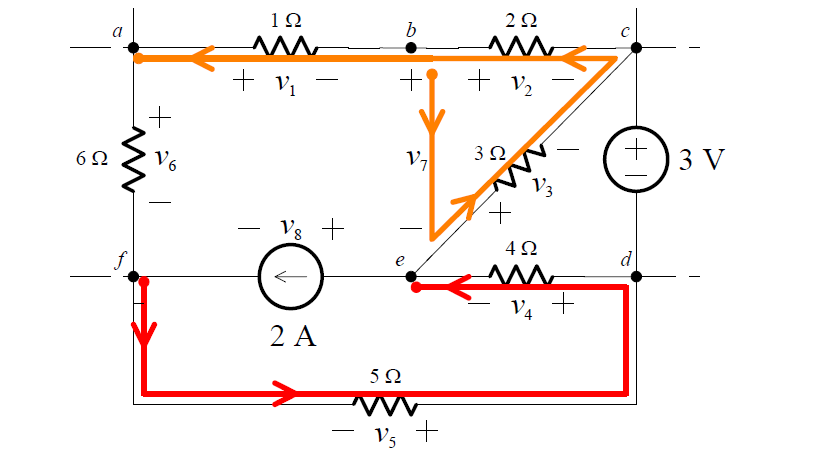
Figure 1 : For example, the paths fabef and fdcef are loops:
Figure 2 : whereas the paths becba and fde are not
Kirchhoff’s Voltage Law (KVL) is essentially the law of conservation of energy. If voltages across elements traversed from – to + are positive in sense, and voltages across elements that are traversed from + to – are negative in sense (or vice versa), then KVL can be stated as follows:
KVL defined as
KVL: Around any loop in a circuit, the voltages algebraically sum to zero.
If there are n elements in the loop then, in symbols, KVL is:
KVL can also be stated as: In traversing a loop, the sum of the voltage rises equals the sum of the voltage drops.
Example 1
In the circuit shown in Figure 1, we select a traversal from – to + to be positive in sense. Then KVL around the loop abcefa gives:
– v1 – v2 + v3 – v8 + v6 = 0
and around loop bcdeb, we have:
– v2 – 3 – v4 + v7 = 0
In this last loop, one of the elements traversed (the element between nodes b and e) is an open-circuit; however, KVL holds regardless of the nature of the elements in the circuit.
Example 2
We want to find the current i, in the one-loop circuit shown below:
The polarities of v1 , v2 , v3 and the direction of i were chosen arbitrarily (the polarities of the 10 V and 34 V sources are given). Applying KVL we get:
10 – v1 – 34 – v2 + v3 = 0
Thus:
v1 + v2 – v3 = -24
From Ohm’s Law:
v1 = 2i
v2 = 4i
v3 = -6i
Substituting these into the previous equation yields:
(2i) + (4i) – (- 6i) = -24
2i + 4i + 6i = -24
12i = -24
i = -2 A
Having solved for i, we now find that:
v1 = 2i = 2(- 2) = -4 V
v2 = 4i = 4(- 2) = -8 V
v3 = -6i = (- 6)(- 2) = 12 V