Barkhausen Criterion

Barkhausen Criterion :

Consider a Inverting Amplifier with Open Loop Gain, A.

The feedback network attenuation factor is β which value is less than unity.

A basic inverting amplifier produces 180⁰ phase shift between input and output, which is shown in below figure.

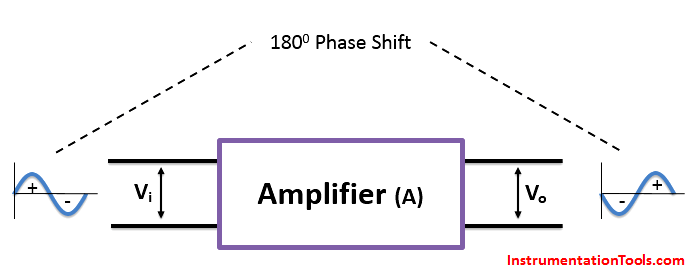
An input voltage Vi is applied to the amplifier and the output Vo value depends on the feedback network.

The basic inverting amplifier output will be 180⁰ phase shift with its input. We need a feedback network which provide a signal such that it must be in-phase with the input of the amplifier. So here we need Positive Feedback network which provides 180⁰ phase shift. The output of Amplifier is connected as input to the feedback network and the feedback network provides 180⁰ phase shift. The output of feedback network will be in-phase with the amplifier input as shown in below figure.

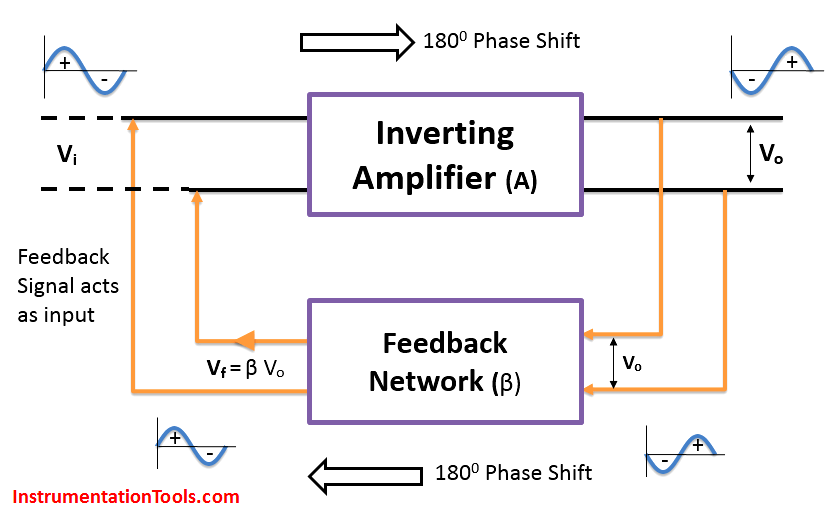
Consider an input voltage Vi is applied to the amplifier and the output voltage will be

Vo = A Vi

The feedback network attenuation factor, β decides the output value of feedback network

Vf = β Vo

By substituting the above two equations, we have

Vf = β A Vi

For the Oscillator, there will be no additional input signal i.e. the feedback signal Vf must act as input to the amplifier. so we have

| A β |  = 1

As discussed above, the feedback network will produce 180⁰ phase shift inaddition to the inverting amplifier such that total phase shift of the loop/circuit will be 360⁰ phase shift.

In this case, the feedback voltage Vf will be sufficient to generate the output oscillations without any external input.

The two conditions discussed are required for a circuit to work as an oscillator are called as Barkhausen Criterion

1. The Total Phase shift of the loop or circuit must be 360⁰ phase shift. The amplifier provides 180⁰ phase shift and the feedback network provides another 180⁰ phase shift. so the total phase shift of the circuit is 360⁰ phase shift.
2. The Product of magnitude of amplifier open loop gain (A) and the magnitude of feedback network factor (β) must be unity. | A β |  = 1

If a circuit satisfies the above two conditions then it will generate constant oscillations with defined frequency & magnitude without using any external input.