How to tune a PID Controller ?

What PID stands for?

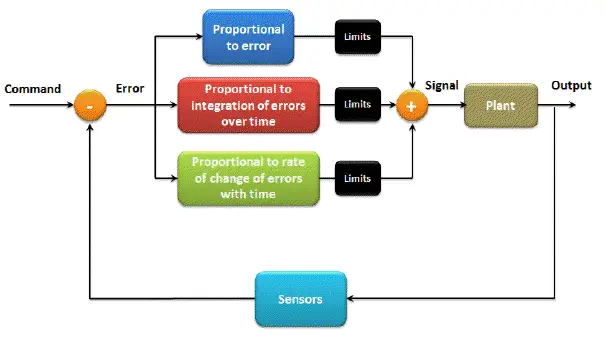
It stands for Proportional, Integral, and Derivative controller. It’s a mathematical description of the way you think. PID helps you automatically achieve your goal, exactly the same way you used to do it manually. This diagram shows a general structure for a PID controller.

So, what do you need to form a PID controller?

You need the following six basic elements:

• Error: It is the difference between your command and the output of the controller.
• Proportional term P: It is a constant directly related to the amount of error. If you have large error, this term gives you a large output. And if you have a small error, it’ll give you a small output, that simple! The P term affects the speed to reach your target.
• Integral term I: It is a constant related to the integration (summation) of errors over time. If your error is increasing, this term gives you a large output. However, if the error is decreasing, the I term gives you a small output. Thus it’s used to fine tune your results, i.e., when you almost reach your goal, the P term cannot serve you anymore (actually it works against you here!), the I term is the one you can count on to drive you error signal to zero.
• Derivative term D: It is a constant related to the rate of change (derivative) of errors with time. What does this mean? It means that if your error signal changes rapidly, i.e., you have a highly dynamic system like a multi copter, the D term will give you higher output to catch up with the changes. On the other hand, if your error changes slowly, like in the room temperature example, the D term won’t find anything fast enough to amplify. Thus it’ll look for your noise signal (which usually has a high frequency) and amplify it to make your life miserable! The D term is a very dangerous controller if it’s not tuned perfectly!
• Limits: You need to limit the output of each of the previous controllers!
• Finally, you need your system of course! Unless you’re satisfied with simulations.

So, how do you tune your PID parameters to the optimal response?

1. After nulling all the parameters, increase the P term so that the output reaches the target in the shortest possible time.
2. If your output starts oscillating, it means you have too much P. Lower your P term until the oscillation disappears. You’ll end up slightly higher or lower than your target. Don’t worry; we’ll fix that in the next step.
3. Now, increase I term slightly until your error goes away. Note that usual I values are very small (in the order of one thousandth for example) and they’re dependent on the update rate of your PID loop. The I term is very useful when you have outside error signals affecting your system (e.g. wind in a multi copter). It drives your error to zero whenever possible.
4. If you feel your output is oscillating and it was not before you adjusted your I term, lower I slightly.
5. For many slow dynamic systems, your job is almost done! You just have to jump to the last step.
   When dealing with highly dynamic systems, however, you need to adjust the D term. If you feel your output “lagging” behind the error variations and trying hard but failing to catch them, increase this term slightly.
6. If your system starts to oscillate with high frequency and small transitions, you probably have too much D term which is amplifying your noise. Decrease D appropriately. If your system,however, has too much noise, it’s better to keep this parameter to zero.
7. Last but not least, watch your limits! If you were changing the previous parameters without any noticeable change in the output, remember that limits cut down your output signal. Increase them probably, but be careful not to burn or saturate your system.

Also Download: PID Controller Simulator